La función φ de Euler (también llamada función totiente) es una función importante en teoría de números. Si n es un número entero positivo, entonces φ(n) se define como la cantidad de enteros positivos menores a n y coprimos con n, es decir, formalmente se puede definir como:​​

φ ( n ) = | { m ∈ N | m ≤ n ∧ m c d ( m , n ) = 1 } | {\displaystyle \varphi (n)=|\{m\in \mathbb {N} \ |\ m\leq n\ \land \ \mathrm {mcd} (m,n)=1\}|}

donde |·| significa la cardinalidad del conjunto descrito. Otra forma de definir el totiente de un número natural n es indicar que es la cantidad de números enteros positivos menores que n tales que el máximo común divisor con respecto a n es igual a 1. La función φ es importante principalmente porque proporciona el tamaño del grupo multiplicativo de enteros módulo n. Más precisamente, φ ( n ) {\displaystyle \varphi (n)} es el orden del grupo de unidades del anillo Z / n Z {\displaystyle \mathbb {Z} /n\mathbb {Z} } . En efecto, junto con el teorema de Lagrange de los posibles tamaños de subgrupos de un grupo, proporciona una demostración del teorema de Euler que dice que a φ ( n ) ≡ 1 ( mod n ) {\displaystyle a^{\varphi (n)}\equiv 1{\pmod {n}}} para todo a coprimo con n. La función φ juega también un papel clave en la definición del sistema de cifrado RSA.

Historia, terminología y notación

Leonhard Euler introdujo la función en 1763.​​​ Sin embargo, en ese momento no eligió ningún símbolo específico para denotarla. En una publicación de 1784, Euler estudió de nuevo la función más a fondo, eligiendo la letra griega π para denotarla: escribió πD para "la multitud de números menores que D, y que no tienen un divisor común con él".​ Esta definición varía de la definición actual de la función totiente en D = 1 pero, por lo demás, es la misma. La notación ahora estándar​​ φ(A) proviene del tratado de Carl Friedrich Gauss de 1801 Disquisitiones arithmeticae,​​ aunque Gauss no usó paréntesis alrededor del argumento y escribió φA. Por lo tanto, a menudo se la llama función phi de Euler o simplemente función phi. En 1879, J. J. Sylvester acuñó el término totiente para esta función,​​ por lo que también se la conoce como función totiente de Euler, totiente de Euler, o el totiente de Euler. El totiente de Jordan es una generalización de la idea de Euler. El cototiente de n {\displaystyle n} se define como n − φ ( n ) {\displaystyle n-\varphi (n)} . Cuenta el número de enteros positivos menores o iguales a n {\displaystyle n} que tienen al menos un factor primo en común con n {\displaystyle n} .

Primeras propiedades y cálculo de la función

Se sigue de la definición que φ ( 1 ) = 1 {\displaystyle \varphi (1)=1} , pues el elemento 1 {\displaystyle 1} sólo puede ser coprimo consigo mismo. Para otros números se cumple que:

φ ( p ) = p − 1 {\displaystyle \varphi (p)=p-1} si p {\displaystyle p} es primo.

φ ( p k ) = ( p − 1 ) p k − 1 {\displaystyle \varphi (p^{k})=(p-1)p^{k-1}} si p {\displaystyle p} es primo y k {\displaystyle k} es un número natural.

φ {\displaystyle \varphi } es una función multiplicativa: si m {\displaystyle m} y n {\displaystyle n} son coprimos, entonces φ ( m n ) = φ ( m ) φ ( n ) {\displaystyle \varphi (mn)=\varphi (m)\varphi (n)} . La primera propiedad se demuestra fácilmente, porque un número primo es coprimo con todos sus números anteriores. Y, por tanto, existen p − 1 {\displaystyle p-1} elementos coprimos con p {\displaystyle p} . En otras palabras, como p {\displaystyle p} es primo sólo tendrá de divisores a sí mismo y a la unidad, la cual está presente en los p − 1 {\displaystyle p-1} números anteriores a p {\displaystyle p} . Para la segunda propiedad, debemos observar que si p {\displaystyle p} es primo sólo sus múltiplos n p {\displaystyle np} menores o iguales que p k {\displaystyle p^{k}} presentan un común divisor con p k {\displaystyle p^{k}} distinto de uno. Esto es, 1 p , 2 p , 3 p , . . . , ( p k − 1 ) p {\displaystyle 1p,\ 2p,\ 3p,\ ...,\ (p^{k-1})p} son los únicos números m {\displaystyle m} tales que m c d ( p k , m ) ≠ 1 {\displaystyle \mathrm {mcd} (p^{k},m)\neq 1} . Como en total hay p k − 1 {\displaystyle p^{k-1}} números que satisfacen esta propiedad, el resto de números entre 1 {\displaystyle 1} y p k {\displaystyle p^{k}} sólo tienen a 1 {\displaystyle 1} como divisor común con p k {\displaystyle p^{k}} . Esto es, φ ( p k ) = p k − p k − 1 = ( p − 1 ) p k − 1 {\displaystyle \varphi (p^{k})=p^{k}-p^{k-1}=(p-1)p^{k-1}} . (Nótese que esta segunda propiedad se cumple porque p {\displaystyle p} es primo. En efecto, si hubiera un m ≠ n p {\displaystyle m\neq np} , m ≥ 2 {\displaystyle m\geq 2} tal que m c d ( p k , m ) = a ≠ 1 {\displaystyle \mathrm {mcd} (p^{k},m)=a\neq 1} , entonces a {\displaystyle a} sería divisor de p k = p ⋅ p . . . p {\displaystyle p^{k}=p\cdot p\ ...\ p} ( k {\displaystyle k} veces); es decir, a {\displaystyle a} sería una potencia (y por consiguiente múltiplo) de p {\displaystyle p} , contradiciendo la suposición inicial m ≠ n p {\displaystyle m\neq np} ). Para demostrar la tercera propiedad, sean A {\displaystyle A} , B {\displaystyle B} , C {\displaystyle C} los conjuntos de enteros positivos que son coprimos y menores que m {\displaystyle m} , n {\displaystyle n} , m n {\displaystyle mn} respectivamente ( entonces | A | = φ ( m ) {\displaystyle |A|=\varphi (m)} , | B | = φ ( n ) {\displaystyle |B|=\varphi (n)} y | C | = φ ( m n ) {\displaystyle |C|=\varphi (mn)} ). Luego, por el Teorema Chino del Resto existe una biyección entre C {\displaystyle C} y A × B {\displaystyle A\times B} , lo que implica que φ ( m n ) = φ ( m ) φ ( n ) {\displaystyle \varphi (mn)=\varphi (m)\varphi (n)} . Con esto, el valor de φ ( n ) {\displaystyle \varphi (n)} puede calcularse empleando el Teorema Fundamental de la Aritmética: si

n = p 1 k 1 ⋯ p r k r {\displaystyle n=p_{1}^{k_{1}}\cdots p_{r}^{k_{r}}}

donde los pj son números primos distintos, entonces

φ ( n ) = ( p 1 − 1 ) p 1 k 1 − 1 ⋯ ( p r − 1 ) p r k r − 1 . {\displaystyle \varphi (n)=(p_{1}-1)p_{1}^{k_{1}-1}\cdots (p_{r}-1)p_{r}^{k_{r}-1}.}

Esta fórmula puede reescribirse de la siguiente manera (conocida como la Fórmula de Producto de Euler):

φ ( n ) = n ∏ p | n ( 1 − 1 p ) {\displaystyle \varphi (n)=n\prod _{p|n}\left(1-{\frac {1}{p}}\right)}

donde los p {\displaystyle p} son los distintos primos que dividen a n {\displaystyle n} .

= Ejemplo de cálculo =

φ ( 36 ) = φ ( 3 2 2 2 ) = 36 ( 1 − 1 3 ) ( 1 − 1 2 ) = 36 ⋅ 2 3 ⋅ 1 2 = 12. {\displaystyle \varphi (36)=\varphi \left(3^{2}2^{2}\right)=36\left(1-{\frac {1}{3}}\right)\left(1-{\frac {1}{2}}\right)=36\cdot {\frac {2}{3}}\cdot {\frac {1}{2}}=12.}

También,

φ ( 36 ) = φ ( 3 2 2 2 ) = ( 3 − 1 ) 3 ( 2 − 1 ) ( 2 − 1 ) 2 ( 2 − 1 ) = 2 ⋅ 3 ⋅ 1 ⋅ 2 = 12. {\displaystyle \varphi (36)=\varphi \left(3^{2}2^{2}\right)=(3-1)3^{(2-1)}(2-1)2^{(2-1)}=2\cdot 3\cdot 1\cdot 2=12.}

Se puede comprobar manualmente que los números coprimos con 36 (o sea, que no son divisibles por 2 ni por 3) son doce: 1, 5, 7, 11, 13, 17, 19, 23, 25, 29, 31, y 35.

= Transformada de Fourier =

El totiente es la transformada de Fourier discreta del mcd, evaluado en 1.​ Sea

F { x } [ m ] = ∑ k = 1 n x k ⋅ e − 2 π i m k n {\displaystyle {\mathcal {F}}\{\mathbf {x} \}[m]=\sum \limits _{k=1}^{n}x_{k}\cdot e^{{-2\pi i}{\frac {mk}{n}}}}

donde xk = mcd(k,n) para k ∈ {1, ..., n}. Entonces

φ ( n ) = F { x } [ 1 ] = ∑ k = 1 n mcd ⁡ ( k , n ) e − 2 π i k n . {\displaystyle \varphi (n)={\mathcal {F}}\{\mathbf {x} \}[1]=\sum \limits _{k=1}^{n}\operatorname {mcd} (k,n)e^{-2\pi i{\frac {k}{n}}}.}

La parte real de esta fórmula es

φ ( n ) = ∑ k = 1 n mcd ⁡ ( k , n ) cos ⁡ 2 π k n {\displaystyle \varphi (n)=\sum \limits _{k=1}^{n}\operatorname {mcd} (k,n)\cos {\tfrac {2\pi k}{n}}}

A diferencia del producto de Euler y la fórmula de la suma del divisor, esta no requiere conocer los factores de n. Sin embargo, implica el cálculo del máximo común divisor de n y todo número entero positivo menor que n, lo que es suficiente para proporcionar la factorización de todos modos.

= Suma de sus divisores =

La propiedad establecida por Gauss,​ de que

∑ d ∣ n φ ( d ) = n , {\displaystyle \sum _{d\mid n}\varphi (d)=n,}

donde la suma es sobre todos los divisores positivos d de n, se puede demostrar de varias maneras (véase función aritmética para conocer las convenciones de la notación). Una prueba es notar que φ(d) también es igual al número de posibles generadores del grupo cíclico Cd; específicamente, si Cd = ⟨g⟩ con gd= 1, entonces gk es un generador para cada coprimo de k a d. Dado que cada elemento de Cn genera un subgrupo cíclico, y todos los subgrupos Cd ⊆ Cn son generados precisamente por elementos φ(d) de Cn, la fórmula es la siguiente.​ De manera equivalente, la fórmula se puede derivar mediante el mismo argumento aplicado al grupo multiplicativo de las raíces de unidad n-ésimas raíces de la unidad y d-ésimas primitivas. La fórmula también se puede derivar de la aritmética elemental.​ Por ejemplo, sea n = 20 y considérense las fracciones positivas hasta 1 con denominador 20:

1 20 , 2 20 , 3 20 , 4 20 , 5 20 , 6 20 , 7 20 , 8 20 , 9 20 , 10 20 , 11 20 , 12 20 , 13 20 , 14 20 , 15 20 , 16 20 , 17 20 , 18 20 , 19 20 , 20 20 . {\displaystyle {\tfrac {1}{20}},\,{\tfrac {2}{20}},\,{\tfrac {3}{20}},\,{\tfrac {4}{20}},\,{\tfrac {5}{20}},\,{\tfrac {6}{20}},\,{\tfrac {7}{20}},\,{\tfrac {8}{20}},\,{\tfrac {9}{20}},\,{\tfrac {10}{20}},\,{\tfrac {11}{20}},\,{\tfrac {12}{20}},\,{\tfrac {13}{20}},\,{\tfrac {14}{20}},\,{\tfrac {15}{20}},\,{\tfrac {16}{20}},\,{\tfrac {17}{20}},\,{\tfrac {18}{20}},\,{\tfrac {19}{20}},\,{\tfrac {20}{20}}.}

Reduciéndolas a términos mínimos:

1 20 , 1 10 , 3 20 , 1 5 , 1 4 , 3 10 , 7 20 , 2 5 , 9 20 , 1 2 , 11 20 , 3 5 , 13 20 , 7 10 , 3 4 , 4 5 , 17 20 , 9 10 , 19 20 , 1 1 {\displaystyle {\tfrac {1}{20}},\,{\tfrac {1}{10}},\,{\tfrac {3}{20}},\,{\tfrac {1}{5}},\,{\tfrac {1}{4}},\,{\tfrac {3}{10}},\,{\tfrac {7}{20}},\,{\tfrac {2}{5}},\,{\tfrac {9}{20}},\,{\tfrac {1}{2}},\,{\tfrac {11}{20}},\,{\tfrac {3}{5}},\,{\tfrac {13}{20}},\,{\tfrac {7}{10}},\,{\tfrac {3}{4}},\,{\tfrac {4}{5}},\,{\tfrac {17}{20}},\,{\tfrac {9}{10}},\,{\tfrac {19}{20}},\,{\tfrac {1}{1}}}

Estas veinte fracciones son todas las k/d ≤ 1 positivas cuyos denominadores son los divisores d = 1, 2, 4, 5, 10, 20. Las fracciones con 20 como denominador son aquellas con numeradores relativamente primos a 20, a saber, 1/20, 3/20, 7/20, 9/20, 11/20, 13/20, 17/20 y 19/20. Por definición, se trata de las φ(20) fracciones con denominador 20. De manera similar, hay φ(10) fracciones con denominador 10 y φ(5) fracciones con denominador 5, etc. Por lo tanto, el conjunto de veinte fracciones se divide en subconjuntos de tamaño φ(d) para cada d que divide 20. Se aplica un argumento similar para cualquier n. La fórmula de inversión de Möbius aplicada a la fórmula de la suma del divisor da

φ ( n ) = ∑ d ∣ n μ ( d ) ⋅ n d = n ∑ d ∣ n μ ( d ) d , {\displaystyle \varphi (n)=\sum _{d\mid n}\mu \left(d\right)\cdot {\frac {n}{d}}=n\sum _{d\mid n}{\frac {\mu (d)}{d}},}

donde μ es la función de Möbius, la función multiplicativa definida por μ ( p ) = − 1 {\displaystyle \mu (p)=-1} y μ ( p k ) = 0 {\displaystyle \mu (p^{k})=0} para cada primo p y k ≥ 2. Esta fórmula también se puede derivar de la fórmula del producto multiplicando ∏ p ∣ n ( 1 − 1 p ) {\textstyle \prod _{p\mid n}(1-{\frac {1}{p}})} para obtener ∑ d ∣ n μ ( d ) d . {\textstyle \sum _{d\mid n}{\frac {\mu (d)}{d}}.}

Un ejemplo:

φ ( 20 ) = μ ( 1 ) ⋅ 20 + μ ( 2 ) ⋅ 10 + μ ( 4 ) ⋅ 5 + μ ( 5 ) ⋅ 4 + μ ( 10 ) ⋅ 2 + μ ( 20 ) ⋅ 1 = 1 ⋅ 20 − 1 ⋅ 10 + 0 ⋅ 5 − 1 ⋅ 4 + 1 ⋅ 2 + 0 ⋅ 1 = 8. {\displaystyle {\begin{aligned}\varphi (20)&=\mu (1)\cdot 20+\mu (2)\cdot 10+\mu (4)\cdot 5+\mu (5)\cdot 4+\mu (10)\cdot 2+\mu (20)\cdot 1\\[.5em]&=1\cdot 20-1\cdot 10+0\cdot 5-1\cdot 4+1\cdot 2+0\cdot 1=8.\end{aligned}}}

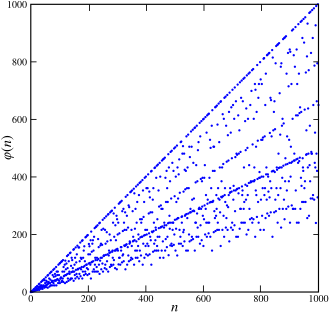
Algunos valores

Los 99 primeros valores de la función vienen escritos en la siguiente tabla, así como gráficamente.

Teorema de Euler

El teorema de Euler establece que si a y n son números coprimos, entonces

a φ ( n ) ≡ 1 mod n . {\displaystyle a^{\varphi (n)}\equiv 1\mod n.}

El caso especial donde n es primo se conoce como el pequeño teorema de Fermat. Esto se deduce del teorema de Lagrange y del hecho de que φ(n) es el orden del grupo multiplicativo de enteros módulo n. El sistema de encriptado RSA se basa en este teorema: implica que el inverso de la función a ↦ ae mod n, donde e es el exponente de cifrado (público), es la función b ↦ bd mod n, donde d, el exponente de descifrado (privado), es el inverso multiplicativo de e módulo φ(n) . La dificultad de calcular φ(n) sin conocer la factorización de n es, por lo tanto, la dificultad de calcular d: esto se conoce como el problema RSA, que se puede resolver factorizando n. El propietario de la clave privada conoce la factorización, ya que una clave privada RSA se construye eligiendo n como el producto de dos números primos grandes (elegidos al azar) p y q. Solo n se divulga públicamente y, dada la dificultad de factorizar números muy largos, se tiene la garantía de que nadie más conocerá la factorización.

Otras fórmulas

a ∣ b ⟹ φ ( a ) ∣ φ ( b ) {\displaystyle a\mid b\implies \varphi (a)\mid \varphi (b)}

n ∣ φ ( a n − 1 ) {\displaystyle n\mid \varphi (a^{n}-1)} ( n , a ∈ N {\displaystyle n,\ a\in \mathbb {N} } , a ≥ 2 {\displaystyle a\geq 2} ) : Sea m = a n − 1 {\displaystyle m=a^{n}-1} . Entonces tenemos que:

mcd ⁡ ( a , m ) = mcd ⁡ ( a , a n − 1 ) = mcd ⁡ ( a , 1 ) = 1 ⇒ a ∈ Z m ∗ ⇒ < a > ⊂ Z m ∗ {\displaystyle \qquad \operatorname {mcd} (a,m)=\operatorname {mcd} (a,a^{n}-1)=\operatorname {mcd} (a,1)=1\ \Rightarrow \ a\in \mathbb {Z} _{m}^{*}\ \Rightarrow \ \,\subset \,\mathbb {Z} _{m}^{*}} . Luego, por el Teorema de Lagrange, | < a > | {\displaystyle ||} divide a | Z m ∗ | {\displaystyle |\ \mathbb {Z} _{m}^{*}\,|} .

{\displaystyle \qquad } Pero a k < m {\displaystyle a^{k} | = n {\displaystyle k 1 y n > 6 tal que 4 ∤ n existe un l ≥ 2n tal que l | φ(an − 1).

φ ( n ) n = φ ( rad ⁡ ( n ) ) rad ⁡ ( n ) {\displaystyle {\frac {\varphi (n)}{n}}={\frac {\varphi (\operatorname {rad} (n))}{\operatorname {rad} (n)}}} ,

{\displaystyle \qquad } donde rad(n) es el radical de n (el producto de todos los primos distintos que dividen n).

∑ d ∣ n μ 2 ( d ) φ ( d ) = n φ ( n ) {\displaystyle \sum _{d\mid n}{\frac {\mu ^{2}(d)}{\varphi (d)}}={\frac {n}{\varphi (n)}}}  ​

∑ 1 ≤ k ≤ n ( k , n ) = 1 k = 1 2 n φ ( n ) para n > 1 {\displaystyle \sum _{1\leq k\leq n \atop (k,n)=1}\!\!k={\tfrac {1}{2}}n\varphi (n)\quad {\text{ para }}n>1}

∑ k = 1 n φ ( k ) = 1 2 ( 1 + ∑ k = 1 n μ ( k ) ⌊ n k ⌋ 2 ) = 3 π 2 n 2 + O ( n ( log ⁡ n ) 2 3 ( log ⁡ log ⁡ n ) 4 3 ) {\displaystyle \sum _{k=1}^{n}\varphi (k)={\tfrac {1}{2}}\left(1+\sum _{k=1}^{n}\mu (k)\left\lfloor {\frac {n}{k}}\right\rfloor ^{2}\right)={\frac {3}{\pi ^{2}}}n^{2}+O\left(n(\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)} (​ citado en​)

∑ k = 1 n φ ( k ) k = ∑ k = 1 n μ ( k ) k ⌊ n k ⌋ = 6 π 2 n + O ( ( log ⁡ n ) 2 3 ( log ⁡ log ⁡ n ) 4 3 ) {\displaystyle \sum _{k=1}^{n}{\frac {\varphi (k)}{k}}=\sum _{k=1}^{n}{\frac {\mu (k)}{k}}\left\lfloor {\frac {n}{k}}\right\rfloor ={\frac {6}{\pi ^{2}}}n+O\left((\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)}  ​

∑ k = 1 n k φ ( k ) = 315 ζ ( 3 ) 2 π 4 n − log ⁡ n 2 + O ( ( log ⁡ n ) 2 3 ) {\displaystyle \sum _{k=1}^{n}{\frac {k}{\varphi (k)}}={\frac {315\,\zeta (3)}{2\pi ^{4}}}n-{\frac {\log n}{2}}+O\left((\log n)^{\frac {2}{3}}\right)}  ​

∑ k = 1 n 1 φ ( k ) = 315 ζ ( 3 ) 2 π 4 ( log ⁡ n + γ − ∑ p primo log ⁡ p p 2 − p + 1 ) + O ( ( log ⁡ n ) 2 3 n ) {\displaystyle \sum _{k=1}^{n}{\frac {1}{\varphi (k)}}={\frac {315\,\zeta (3)}{2\pi ^{4}}}\left(\log n+\gamma -\sum _{p{\text{ primo }}}{\frac {\log p}{p^{2}-p+1}}\right)+O\left({\frac {(\log n)^{\frac {2}{3}}}{n}}\right)} &thinsp,​

{\displaystyle \qquad } donde γ es la constante de Euler-Mascheroni.

∑ mcd ⁡ ( k , m ) = 1 1 ≤ k ≤ n 1 = n φ ( m ) m + O ( 2 ω ( m ) ) {\displaystyle \sum _{\stackrel {1\leq k\leq n}{\operatorname {mcd} (k,m)=1}}\!\!\!\!1=n{\frac {\varphi (m)}{m}}+O\left(2^{\omega (m)}\right)} ,

{\displaystyle \qquad } donde m > 1 es un entero positivo y ω(m) es el número de factores primos distintos de m.​​

= Identidad de Menon =

En 1965, P. Kesava Menon demostró que

∑ mcd ⁡ ( k , n ) = 1 1 ≤ k ≤ n mcd ⁡ ( k − 1 , n ) = φ ( n ) d ( n ) {\displaystyle \sum _{\stackrel {1\leq k\leq n}{\operatorname {mcd} (k,n)=1}}\!\!\!\!\operatorname {mcd} (k-1,n)=\varphi (n)d(n)} , donde d(n) = σ0(n) es el número de divisores de n.

= Fórmulas que involucran la proporción áurea =

Schneider​ encontró un par de identidades que conectan la función totiente, el número áureo y la función de Möbius μ(n). En esta sección, φ(n) es la función totiente y ϕ = 1 + √5/2 = 1.618... es la proporción áurea. Se tiene que:

ϕ = − ∑ k = 1 ∞ φ ( k ) k log ⁡ ( 1 − 1 ϕ k ) {\displaystyle \phi =-\sum _{k=1}^{\infty }{\frac {\varphi (k)}{k}}\log \left(1-{\frac {1}{\phi ^{k}}}\right)}

y

1 ϕ = − ∑ k = 1 ∞ μ ( k ) k log ⁡ ( 1 − 1 ϕ k ) . {\displaystyle {\frac {1}{\phi }}=-\sum _{k=1}^{\infty }{\frac {\mu (k)}{k}}\log \left(1-{\frac {1}{\phi ^{k}}}\right).}

Si se restan, se obtiene

∑ k = 1 ∞ μ ( k ) − φ ( k ) k log ⁡ ( 1 − 1 ϕ k ) = 1. {\displaystyle \sum _{k=1}^{\infty }{\frac {\mu (k)-\varphi (k)}{k}}\log \left(1-{\frac {1}{\phi ^{k}}}\right)=1.}

La aplicación de la función exponencial a ambos lados de la identidad anterior produce una fórmula de producto infinito vinculada a e:

e = ∏ k = 1 ∞ ( 1 − 1 ϕ k ) μ ( k ) − φ ( k ) k . {\displaystyle e=\prod _{k=1}^{\infty }\left(1-{\frac {1}{\phi ^{k}}}\right)\!\!^{\frac {\mu (k)-\varphi (k)}{k}}.}

La demostración se basa en las dos fórmulas siguientes

∑ k = 1 ∞ φ ( k ) k ( − log ⁡ ( 1 − x k ) ) = x 1 − x y ∑ k = 1 ∞ μ ( k ) k ( − log ⁡ ( 1 − x k ) ) = x , para 0 < x < 1. {\displaystyle {\begin{aligned}\sum _{k=1}^{\infty }{\frac {\varphi (k)}{k}}\left(-\log \left(1-x^{k}\right)\right)&={\frac {x}{1-x}}\\{\text{y}}\;\sum _{k=1}^{\infty }{\frac {\mu (k)}{k}}\left(-\log \left(1-x^{k}\right)\right)&=x,\qquad \quad {\text{ para }}02} . La función generadora de la serie de Lambert es​

∑ n = 1 ∞ φ ( n ) q n 1 − q n = q ( 1 − q ) 2 {\displaystyle \sum _{n=1}^{\infty }{\frac {\varphi (n)q^{n}}{1-q^{n}}}={\frac {q}{(1-q)^{2}}}}

que converge para | q | < 1. Ambas fórmulas se demuestran mediante manipulaciones de series elementales y las fórmulas para φ(n).

Tasa de crecimiento

En palabras de Hardy & Wright, el orden de φ(n) es "siempre «casi n»".​ Primero​

lim sup φ ( n ) n = 1 , {\displaystyle \lim \sup {\frac {\varphi (n)}{n}}=1,}

pero como n tiende a infinito,​ para todo δ > 0

φ ( n ) n 1 − δ → ∞ . {\displaystyle {\frac {\varphi (n)}{n^{1-\delta }}}\rightarrow \infty .}

Estas dos fórmulas se pueden probar usando poco más que las fórmulas para φ(n) y la función suma de divisores σ(n). De hecho, durante la demostración de la segunda fórmula, la desigualdad

6 π 2 < φ ( n ) σ ( n ) n 2 < 1 , {\displaystyle {\frac {6}{\pi ^{2}}} n e γ log ⁡ log ⁡ n + 3 log ⁡ log ⁡ n para n ≥ 3 {\displaystyle \varphi (n)>{\frac {n}{e^{\gamma }\;\log \log n+{\frac {3}{\log \log n}}}}\quad {\text{ para }}n\geq 3}

y

φ ( n ) < n e γ log ⁡ log ⁡ n para infinitamente muchos n . {\displaystyle \varphi (n) 1020 y que ω(n) ≥ 14.​ Además, Hagis demostró que si 3 divide a n, entonces n > 101937042 y ω(n) ≥ 298848.​​

= Conjetura de Carmichael =

Este enunciado establece que no hay ningún número n con la propiedad de que para todos los demás números m, m ≠ n, φ(m) ≠ φ(n). Véase el teorema de Ford más arriba. Como se indica en el artículo principal, si hay un solo contraejemplo a esta conjetura, debe haber un número infinito de contraejemplos, y el más pequeño tiene al menos diez mil millones de dígitos en base 10.​

= Hipótesis de Riemann =

La hipótesis de Riemann es verdadera si y solo si la desigualdad

n φ ( n ) < e γ log ⁡ log ⁡ n + e γ ( 4 + γ − log ⁡ 4 π ) log ⁡ n {\displaystyle {\frac {n}{\varphi (n)}}

Fuente: Wikipedia

Este artículo ha sido adaptado de Wikipedia bajo licencia Creative Commons.